Machine learning for parameter estimation
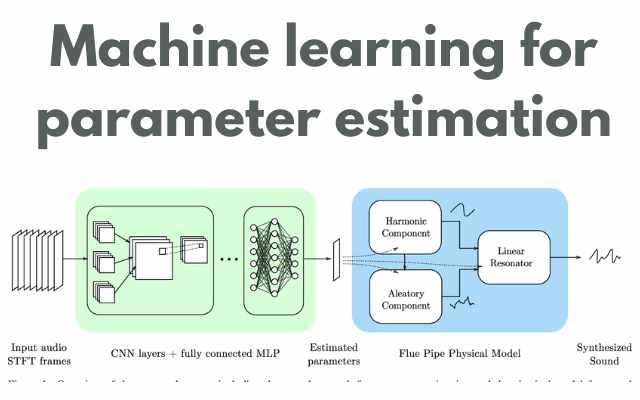
Machine learning for parameter estimation: Parameter estimation is an important task in many fields, including engineering, physics, biology, and economics. The goal is to estimate the parameters of a model that best fit the observed data. Machine learning algorithms can be used for parameter estimation in situations where traditional methods are not suitable or fail to produce accurate results. This article will discuss the use of machine learning for parameter estimation, including the types of models and algorithms used, as well as the advantages and limitations of this approach.
What is parameter estimation?
Parameter estimation is the process of determining the parameters of a model that best fit the observed data. In mathematical modeling, a model is a simplified representation of a real-world system that can be used to make predictions or understand the behavior of the system. The parameters of the model are variables that are not known a priori and must be estimated from the data.
For example, consider a simple linear regression model that relates the independent variable x to the dependent variable y. The model can be expressed as:
y = mx + b
where m and b are the parameters that need to be estimated from the data. Given a set of observed values of x and y, the goal is to find the values of m and b that best fit the data.
What are the traditional methods for parameter estimation?
There are several traditional methods for parameter estimation, including the method of least squares, maximum likelihood estimation, and Bayesian inference. These methods are based on statistical principles and rely on assumptions about the distribution of the data and the model.
The method of least squares is a common approach that minimizes the sum of the squared differences between the observed data and the predicted values of the model. This method is used for linear regression and other linear models.
Maximum likelihood estimation is a method that maximizes the likelihood function, which is a measure of how likely the observed data is given the parameters of the model. This method is used for nonlinear models and can be extended to include more complex models and data structures.
Bayesian inference is a method that combines prior knowledge about the parameters with the observed data to obtain a posterior distribution of the parameters. This method is useful when there is uncertainty about the parameters and can be used to estimate the parameters of complex models.
What are the limitations of traditional methods for parameter estimation?
Traditional methods for parameter estimation can be computationally intensive and require a significant amount of expertise to implement and interpret. These methods also rely on assumptions about the distribution of the data and the model, which may not be accurate or may not hold for the observed data.
Another limitation of traditional methods is that they may not be suitable for complex models or large datasets. For example, nonlinear models may have multiple local minima in the objective function, which can make it difficult to find the global optimum. In addition, traditional methods may not be scalable to large datasets, which can result in long computation times and memory constraints.
How can machine learning be used for parameter estimation?
Machine learning algorithms can be used for parameter estimation by training models on the observed data and optimizing the model parameters to minimize the error between the predicted and observed values. There are several types of machine learning models that can be used for parameter estimation, including regression models, neural networks, and support vector machines.
Regression models are a class of models that relate the input variables to the output variable. These models can be linear or nonlinear and can be used for both continuous and categorical data. Regression models can be trained using a variety of techniques, including gradient descent, stochastic gradient descent, and Newton’s method.
Neural networks are a class of models that are inspired by the structure and function of the human brain. These models consist of layers of interconnected neurons that can learn to represent complex patterns in the data. Neural networks can be used for both supervised and unsupervised learning and can be trained using back propagation, a gradient-based optimization algorithm that adjusts the weights of the neurons to minimize the error between the predicted and observed values.
Support vector machines (SVMs) are a class of models that separate the data into different classes using a hyperplane. SVMs can be used for both linear and nonlinear classification and regression problems. SVMs are trained by maximizing the margin between the hyperplane and the data points, which can be done using a variety of optimization algorithms, including gradient descent and sequential minimal optimization.
Advantages of machine learning for parameter estimation
There are several advantages to using machine learning for parameter estimation. First, machine learning algorithms can be used for complex models and large datasets that may not be suitable for traditional methods. Second, machine learning algorithms can learn from the data and improve their performance over time, which can result in more accurate and reliable parameter estimates. Third, machine learning algorithms can be used for both supervised and unsupervised learning, which can be useful for exploring the data and identifying patterns and relationships.
Limitations of machine learning for parameter estimation
There are also limitations to using machine learning for parameter estimation. One limitation is that machine learning algorithms can be computationally intensive and require a significant amount of computational resources, especially for large datasets or complex models. Another limitation is that machine learning algorithms can be prone to overfitting, which occurs when the model is too complex and fits the noise in the data instead of the underlying pattern. Overfitting can be mitigated by using regularization techniques or by using a larger dataset.
- How to use artificial intelligence and machine learning in your business or personal projects
- Machine Learning : An Introductory Review Of Machine Learning
- Which websites, books, or lessons are the best for learning programming?
FAQ:
Q: What is parameter estimation in machine learning?
A: Parameter estimation is the process of finding the optimal values for the parameters in a machine learning model, such as the weights in a neural network or the coefficients in a linear regression model.
Q: Why is parameter estimation important in machine learning?
A: Parameter estimation is crucial because it enables machine learning models to make accurate predictions. By finding the optimal values for the parameters, the model is able to fit the data more closely and produce more reliable results.
Q: What are some common methods for parameter estimation in machine learning?
A: Some common methods for parameter estimation include gradient descent, stochastic gradient descent, and maximum likelihood estimation.
Q: How do you choose the best method for parameter estimation?
A: The choice of method depends on the specific problem at hand and the characteristics of the data being analyzed. Some methods may be more appropriate for large datasets, while others may be better suited for models with many parameters.
Q: How do you evaluate the accuracy of a machine learning model?
A: The accuracy of a machine learning model can be evaluated using a variety of metrics, such as mean squared error, root mean squared error, or R-squared.
Conclusion:
Parameter estimation is a critical component of machine learning. By finding the optimal values for the parameters in a model, it is possible to create more accurate and reliable predictions. There are a variety of methods available for parameter estimation, including gradient descent and maximum likelihood estimation. The choice of method depends on the specific problem at hand and the characteristics of the data being analyzed. Finally, the accuracy of a machine learning model can be evaluated using various metrics, and the evaluation process should be carefully designed to ensure that the model is performing as intended.






